Геометрия

Геометрия	Методическая копилка
Прямые и плоскости в пространстве
Занятие 1 .	Взаимное расположение двух прямых в пространстве.
Занятие 2	Признак параллельности прямой и плоскости.
Занятие 3	Взаимное расположение двух плоскостей.
Занятие 4	Теорема о трёх перпендикулярах.
Занятие 5	Двугранный угол. Линейный угол двугранного угла.
Многогранники
Занятие 6	Понятие о многограннике. Правильные многогранники.
Занятие 7	Прямая и правильная призма. Параллелепипед.
Занятие 8	Пирамида. Усечённая пирамида.
Занятие 9	Решение задач по теме "Многогранники".
Тела и поверхности вращения
Занятие 10	Тела и поверхности вращения
Занятие 11	Цилиндр. Конус.
Занятие 12	Сфера. Шар.
Объемы тел и площади их поверхности
Занятие 13	Объём параллелепипеда, призмы, цилиндра, пирамиды и конуса.
Занятие 14	Площади поверхностей призмы, пирамиды, цилиндра и конуса.
Занятие 15	Объём шара и его частей. Площадь сферы.
Координаты и векторы.
Занятие 16	Координаты вектора. Скалярное произведение векторов.
Занятие 17	Угол между векторами.
Занятие 18	Векторное произведение векторов.

Занятие 12. Сфера. Шар.

Сфера и шар

Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии R от данной точки О.

Радиус - отрезок, соединяющий центр О сферы с любой её точкой М.
Диаметр D - отрезок, соединяющий две точки сферы и проходящий через ее центр. Соответствующие концы диаметра называются диаметрально противоположными. Диаметр D сферы равен двум радиусам: D = 2R.
Шар - тело, ограниченное сферой. Центр, радиус, диаметр сферы являются также центром, радиусом, диаметром шара. Шар радиуса R с центром в точке О содержит все точки пространства, которые расположены от точки О на расстоянии не больше, чем R.

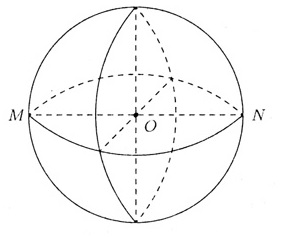O - центр сферы; R - радиус сферы;
MN- диаметр; OM=ON-радиус

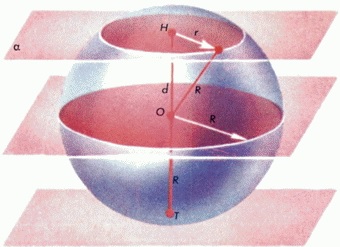
Сечения сферы (шара) плоскостью являются окружностями (кругами).
Касательная плоскостью к сфере - плоскость, имеющая единственную общую точку со сферой.

1) Когда расстояние от центра шара до плоскости меньше радиуса, то плоскость пересекает шар.
Сечение шара этой плоскостью - круг.
2) Когда расстояние от центра шара до плоскости равно радиусу шара, то плоскость является касательной.
3) Когда расстояние от центра шара до плоскости больше радиуса, то плоскость и шар не имеют общих точек.
Прямая, касающаяся сферы - это прямая, которая имеет единственную общую точку со сферой.
Существует два вида касания: внутреннее и внешнее.

Проверка усвоения знаний.

1. Сколько сфер можно провести:
а) через одну и ту же окружность;
б) через окружность и точку, не принадлежащую её плоскости.

2. Сколько сфер можно провести через четыре точки, являющиеся вершинами:
а) квадрата;
б) равнобедренной трапеции;
в) ромба?

3. Верно ли, что через любые две точки сферы проходит один большой круг?

4. Через какие две точки сферы можно провести несколько окружностей большого круга?

5. Как должны быть расположены две равные окружности, чтобы через них могла пройти сфера того же радиуса?

Решить задачи

1. Секущая плоскость делит радиус R, перпендикулярный ей в отношение 4:1, считая от центра. Определите радиус получившийся в сечении окружности.

2. Шар с центром в точке О касается плоскости. Точка А лежит в этой плоскости. Найдите расстояние от точки А до точки касания, если её расстояние от центра шара равно 25 см, а радиус шара равен 15 см.

3. В шаре радиуса 26 см на расстоянии 10 см от центра проведена секущая плоскость. Найдите плоскость сечения.